Introduction
The key to market sizing and brainteaser questions is familiarity, so I recommend carefully going through the 19 questions below to dominate the following areas: market sizing, calculations with multiple steps, mental maths drills and statistics (conditional probability plus configurations).
But remember that brainteasers appear later in the application process so you are more likely to get knocked out by another obstacle earlier on. Therefore, I first recommend considering the divide and conquer strategy laid out below that comprises the “Intern Game Plan”:
- CV. Finalizing your CV and then boosting it e.g. by completing online courses so that you can apply early.
- Cover Letter. Writing a solid cover letter or pre-application question response by honing your communication skills and using insights gained through networking.
- Online Tests. Practising and documenting situational judgement and psychometric tests (numerical, verbal and logical).
- Video Interview & Competencies. Developing an unbeatable set of competency question responses, cracking the HireVue video interview algorithm and first round interview.
- Technicals. Never getting caught out on a technical question.
- Commercial awareness. Building a repertoire of responses to ‘tell me about a recent news story’ and ‘tell me about a recent deal’.
- Assessment Centre (AC). Preparing for ACs and being able to present a killer PowerPoint deck during an Assessment Centre.
- Resilience. Focusing on your circle of influence in the face of rejection while preventing application season burnout.
The final point before delving into each brainteaser category is that if you’re asked a similar brainteaser that you’ve heard before, you could say I’ve been asked this before, but my advice is to visit homepage go ahead with it and problem solve thoroughly. They want logical thinking and this, combined with nervousness, is best borne out of familiarity so the fact that you have gone through the question before should be used to your advantage.
Experience the evolutionary journey of Patek Philippe replica watches; compare patek philippe nautilus replica vs real, uncovering luxury at affordable prices.Market Sizing
Although usually reserved for consulting, market sizing questions appear in interviews for a wide variety of industries because of the logical thinking required.
The hack to answering any market sizing questions in the most straightforward manner is coming up with an overall equation that will lead to your answer. Then walk through that single-lined equation with the interviewer while remembering to round numbers to make them convenient to use. Within that single line equation you come up with, it is also useful to find one component that can be disaggregated e.g. lovers vs haters of oat milk or wealthy vs poor households as demonstrated below.

Q1. What is the UK market size of oat milk in revenue per year for the UK?
The overall equation: Oat milk revenue per year=#People in the UK*Quantity per person per year * Cost per unit.
[I] Number of people in the UK.
Disaggregating one of the variables is key to showing your ability and thinking in a more comprehensive manner.
E.g. #people in this case (disaggregated based on their regularity of use), or it could be #mattresses (large family homes, small family homes, hotels, hospitals), #pigs in a country (food, medicines, lard, leather).
Disaggregate the ~65m people in the UK into 3 estimated segments.
- [a] People that never use oat milk; 45m
- [b] People that occasionally use oat milk; 15m
- [c] Oat milk lovers; 5m
[II] Quantity per person (follows on from disaggregation).
- [a] 0ml per day
- [b] 50ml per day × 360 days = 18litres per year. Round to 20litres. 20litres × 15m = 300m litres.
- [c] Oat milk lovers might drink 4x segment b’s amount. 20litres × 4 = 80 litres per year. 80 litres × 5m = 400m litres. This 200ml consumed by oat milk lovers might involve 150ml in cereal and another 50ml in coffee per day.
Total population consumption=300m + 400m=700m litres per year
[III] Finding revenue per year.
Cost of a litre of almond milk ~£1
Oat milk revenue per year = 700mx£1=£0.7bn
The beauty of this approach is that if you want to, you can dig deeper into each respective component and add more complexities but this is not usually necessary for investment banking interviews.
Q2. How many electric cars are there in China?
#Electric cars in China = #households*cars per household*cars that are electric
Number of households
The number of households in China can be found by dividing the total population by the number of people per household.
#Households=1.5bn/3 (total population divided by average people per household)
#Households=~ 500m
It is important to justify your assumptions so in this case, you could say that three people per household balances single residence households with families that live alongside grandparents or couples that have more than one child in China considering the one-child policy has now been dropped.
Cars per household
This is an opportunity to disaggregate cars per household into household wealth brackets. Where ‘w.’ denotes wealth and ‘c.’ denotes the number of cars for that segment:
Cars per household=%w.low*c.low+%w.med*c.med+%w.high*c.high
Let’s assume low wealth households have no cars and constitute 50% of the population, medium wealth households have one car per household and constitute 40% of the population, while the high wealth households have two cars each and constitute the final 10% of the population.
Cars per household=0.5*0+0.4*1+0.1*2=0.6
For simplicity, it’s worth simplifying this to 0.5 cars per household.
The proportion of cars that are electric
This is another opportunity to disaggregate cars into 2nd hand and new cars although due to the pressure of interviews, disaggregating just one of the components is usually enough. Let’s assume that 80% of the cars in China are bought 2nd hand while 20% are newly made with none of the 2nd hand cars being electric but 10% of the new cars being electric.
Proportion electric = %[2nd hand]*%[2nd electric]+%[new]*%[new electric]
Proportion electric = 0.8*0.0 + 0.2*0.1
Based on these assumptions, the proportion of total cars that are electric = 0.02
Bringing it all together
#Electric cars in China = 500m*0.5*0.02 = 500m*0.01=500m*(1/100)
So approximately 5m of the cars in China are electric. This seems fairly reasonable considering Wikipedia reports that China had 4.6 million units of electric cars as of December 2020.
Q3. How many mattresses are sold in the US?
#Mattresses sold in US = (#households*mattresses per household + #hotels*mattresses per hotel)*%replaced.
The third and final country in this series of examples centres around the US, which has a population of about 330 million people.
For a consulting interview, you may be given a lot more time and therefore go into more detail, but considering you may only get a minute to think about this during an investment banking interview, balancing simplification with some thoughtful disaggregating factor is key (in this case we’ll disaggregate homes and hotels).
Number of households
There are roughly 330m people in the USA, and assuming an average household size of three:
330m/3=110m which can be rounded down to 100m
Number of mattresses per household
Assuming two of the three people in each household share a mattress (as a couple), we can say there are two mattresses per household.
Number of hotels
For simplicity, we focus on hotels for alternative mattress use. Assuming there is one hotel per 20 households, we can say there are around 50,000 hotels in the US.
Number of mattresses per hotel
This component seems to offer a good opportunity for disaggregation so we might split up hotels into small, medium and large categories like the following:
- 50% being small hotels that have 50 beds.
- 40% being medium hotels that have 500 beds.
- 10% being large hotels that have 2000 beds
So #mattresses per hotel =0.5*50+0.4*500+0.1*2000=25+200+200=425 which we can round down to 400.
Percentage of mattresses replaced each year
Assuming mattresses have a lifespan of 10 years, we can say that 10% of mattresses in the US will be replaced per year.
#Mattresses sold in US = (100m*2+50k*400)*(1/10)
To simplify the calculation above, especially if you are not given a piece of paper, first divide the 100m and 400 by 10:
=10m*2+50k*40=20m+2m=22m mattresses bought in the US per year.
A final technique is to say if given more time, I would also consider hospital beds and mattresses used in caravans among other details.
Calculations with multiple steps

Q4. You have a tap with a 300ml and 500ml cup. How do you get exactly 400ml of water?
Fill the 300ml cup and pour it into the 500ml cup. Then refill the 300ml and pour into a 500ml cup until it’s full. That leaves 100ml in the 300ml cup and 500ml in the 500ml cup. Empty the 500ml cup and pour the 100ml from the 300ml cup into the 500ml cup.
Then refill the 300ml cup and pour it into the 500ml cup. Voila – you have 400ml.
Q5. Imagine you have a large cube structure made up of mini cubes (10x10x10=1000 cubes). Then imagine that this large cube is dipped into red paint so that everything except the top layer is covered. How much is covered in red?.
First we should calculate how many squares are in the inner layer of the massive cube: 8x8x8=64×8=60×8+4×8=480+32=512
Now, 1000-512=1000-512=488 is on the outside.
So 488-8×8 (top side not covered in red)=488-64=424 that get stained in red.
This leads to another point: do not get too confident. Communicate your calculations clearly otherwise you’ll slip up. You might be comfortable in your chair at the moment reading this, but when your heart is racing faster than normal in that interview, you need to keep humble and thorough.
Q6. What is the reflex angle between the handles of a clock at 3:30pm?
The key to this question is realising that the hour hand moves one half the way between three and four by the time the clock reads 3:30pm. There are 12 hours on the face of the clock and 360 degrees / 12 = 30 degrees so the hour hand would have moved 15 degrees.
Acute angle between hands at 3:30pm = 90-15=75
Therefore reflex angle = 360-75=285 degrees.
Q7. Four interns from different companies need to cross a bridge that only has space for two people at once to get to the club on time…
…They have one flashlight and 14 minutes to get there before their queue jump expires. The quant trader and consultant can cross in 1 minute, the asset manager can cross in 5 minutes and the investment banker can cross in 10 minutes. How can they make it before their queue jump expires in time for the club?
The quant trader and consultant cross first (1 minute total), before the quant trader returns (2 minutes), passing the flashlight to the asset manager and investment banker who walk across (12 minutes) before they pass it to the consultant who walks back (13 minutes) and returns with the quant trader (14 minutes).
Q8. There are three boxes of chocolates. In each box, there are either dark, brown or white chocolate…
…The boxes are labelled “dark”, “brown” and “white” but every box is mislabelled. What is the least number of boxes you need to open to know which boxes contain each of the three types?
One. Once you open one of the boxes, you know which chocolates that box corresponds to and you can work the rest out considering you know that all the other boxes are mislabeled.
Q9. You own a cattery. At a particular point in time, if you put one cat per room, you have one cat without a room…
…If you put two cats per room, you have two rooms spare. How many cats and rooms do you have at this particular point in time?
For this question, rather than trying to deduce the answer algebraically, you could simply use trial and error. We know there must be an even number of cats since when paired, there are none remaining.
If you had two cats and two rooms, the first condition is not satisfied, but the second is.
If we move to four cats and two rooms, the first condition isn’t satisfied, nor the second.
If we move to four cats and three rooms, the first condition is satisfied and so is the second. So the answer is four cats and three rooms.
Mental Maths

If I could go back to application season, I would spend at least 15 minutes a day training my mind to rapidly answer mental maths questions because when this component comes up, whether at an investment bank or other division you apply to, such practice will massively set you apart. Crunching numbers quickly is something that can be trained like a muscle and I recommend using an app that gamifies this process.
It is easy for people that have good mental maths ability to get confident here but confidence is your greatest liability. You probably won’t have a piece of paper to work this out, so you must do it verbally.
Also, if they say you get it wrong, you must continue and leave it. Your mind will begin running rampage with distracting thoughts, but you need to keep calm in those moments more than any other.
I have found myself and seen many others get this wrong even though we think to ourselves that out of all the questions, I’m sure I’ll handle a simple maths one. Remember, the nerves mean your brain is going into overdrive. You need to focus and be patient in your thoroughness.
DO NOT start rushing or speaking fast – instead, take a slow breath to reduce the nerves (and ego) before answering.
Q10. What is 64*98?
64*90=60*90+4*90=5400+360
5400+360=5760
64*8=60*8+4*8=480+32
480+32=512
5760+512=6272
Quick reality check: 60*100=6000 so at least I haven’t gone too far off in case there is a mistake.
Q11. Make 84 using the following operators: +, -, *, /, (, ) and the following numbers: 4, 4, 12 and 12.
(4+4)*12-12=84
Q12. How many times do the hands of a clock overlap in a day?
As if looking at the clock and two hands as a race from the start till the end of the day: we start at midnight where the number of overlaps is zero and the minute hand makes its first round. The hands overlap once the minute hand reaches 1:05. Then it overlaps again when the time reaches 2:10. As you can see, it’s not as simple as overlapping 24 times because more than 1/12th of the day has passed by the time there have only been two overlaps.
You may quickly see that 5 minutes is accumulated after one hour (before the overlap takes place), so after 12 hours, 60 minutes extra would have accumulated before the overlap takes place. Via the same logic, by 24 hours, 120 minutes would have accumulated before the final overlap takes place. So when the experiment is cut off at midnight the next day, only 22 overlaps would have been reached since the minute’s hand has outpaced the starting position overlap by two hours.
Alternatively, you could calculate this algebraically: in T hours, the minute’s hand would complete T laps round the clock. In T hours, the hour’s hand would complete T/12 laps round the clock. For the first overlap of the hands, the minute hand would have lapped the hour hand by one round of the clock. For the second time they overlap the minute’s hand would have overlapped the hour’s hand by two rounds of the clock.
In a more general form, for the Nth time they overlap, the minute’s hand would have overlapped the hour’s hand by N rounds of the clock. So T=T/12+N
Setting T=24 which is when the ‘race’ ends at midnight, 24 hours from the start, we can find N, the number of overlaps, as:
24=24/12+N
24=2+N
N=22
Q13. How many pounds are required to take a stack from the floor to the ceiling
If you aren’t given any measurements and must estimate the thickness of the pound and average height of the ceiling, you can say a pound is about 0.25cm (2.5mm) thick and a room is about 2.5m high (2500mm). This makes for the convenient calculation of 2500/2.5=25000/25=1000.
The actual thickness of a pound is 2.8mm and the standard height of a room is 2.4m according to this website, so the actual answer may be slightly less at around 860 pound coins.
Q14. What’s the sum of natural numbers (positive whole numbers) from 1 to 100?
Many people preparing for interviews may have covered this in e.g. A-Level Maths during school, but for those that didn’t take Maths, the trick here is to find the following pattern:
0+100=100
1+99=100
2+98=100
3+97=100
..All the way down to…
49+51=100
With 50 being in the middle with no pair.
So rather than counting each number consecutively, you can simply calculate 100*50 pairs + 50 = 5050.
Note that there are still 50 pairs even though 50 is on its own because we counted 0+100 at the beginning.
Even if you have covered this topic of sequences in Maths before, there is a chance you may forget the formula and I think the formula is less impressive than finding the pattern and working your way up from first principles to find the answer.
Statistical Questions

Q15. You have 10 coins (five £1 coins and five £2 coins) and two containers…
…How would you divide the coins to maximise the chance of randomly selecting a £2 coin if choosing one coin from each container?
Place one £2 coin in container A and all the other coins in container B. The probability of selecting a £2 coin = 0.5*1+0.5*(4/9)=0.5+0.22=0.72.
Q16. Imagine there is a disease that has a chance of occurring once in every 1 million people…
…and the test used to detect the disease is wrong 1% of the time. What is the probability you have the disease if you test positive?
The probability you have the disease if you test positive is a conditional probability calculation which is a very common application of statistics required in brain teaser questions. If you find this first method of calculation confusing, I strongly recommend checking out the more visual technique of probability trees explained further down this page.
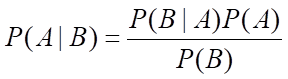
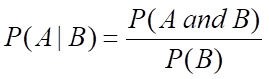
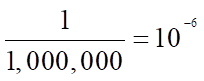
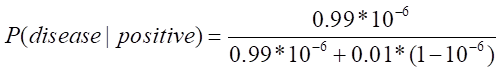
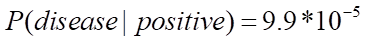
Even though the test seems accurate being only wrong 1% of the time, due to how rare the disease is, you’re much more likely to not have the disease and test positive than to have the disease (0.0001% and 0.000001% respectively which is 100 times more likely).
If you found the conditional probability formula confusing, a more visual calculation method is to use frameworks like a sample space. A sample space represents all possible outcomes in an experiment. Three common visual techniques for the sample space include:
- Lists
- Tables
- Tree diagrams
For a simple experiment where two coins are tossed and you need to map the sample space representing all possible outcomes, the first two methods of visualisation might look like the following:

Although the table method of outcome spaces is more compact than the tree diagram method, most people including myself find the tree diagram easier to grasp when first approaching these conditional probability problems. Below is the disease test calculation using the probability tree diagram.

Q17. Imagine if you had 10 blue socks and 10 red socks in a drawer…
…f you choose two socks at random with your eyes closed, what is the probability of choosing two socks of the same colour?
By symmetry, we know P(blue pair)=P(red pair) so let’s focus on the probability of a blue pair to start with.
For the first sock selected, there is a 1/2 chance of selecting a blue sock.
For the second sock, there is now a 9/19 chance of selecting blue again because if we first picked up a blue sock, this is not replaced when we choose the second sock.
P(blue pair)=(1/2)*(9/19)=9/38=P(white pair)
P(any pair)=P(blue pair)+P(white pair)
P(any pair)=(9/38)+(9/38)=18/38=9/19 (or 47.4%)
Q18. You are shown three boxes…
…One of these boxes contains a diamond worth £100k while the other boxes contain a block of coal. You choose one of the boxes and are shown that one of the other boxes contain a block of coal. You are then offered to either switch or keep the box you were just given: would you switch?
The correct answer is to switch. Based on probabilities, there was a 1/3 chance that the box you first selected contained the diamond. Now that you were shown one of the other boxes definitely does not contain the diamond, the chance that the remaining box contains the diamond shoots up to 2/3. So statistically speaking, you would be doubling your chances of success from 1/3 to 2/3 by switching your box.
Q19. 32 people enter a table tennis tournament involving five rounds…
…where each round consists of two players going against each other and the winner staying onto the next round leaving one player as the winner at the end. Each player’s probability of winning a match is 50% and pairings are random. For two given players: What is the probability they play each other in the final round and that they play each other at all?
First, we need to be familiar with a basic understanding of statistical configurations for this question:
Before looking at permutations i.e. P(n,r) and combinations i.e. C(n,r), it is important to know that an exclamation mark means ‘factorial’:
n!=n*(n-1)*(n-2)….*1
E.g. 3!=3*2*1=6
Permutations: The number of different arrangements of n things taken r at a time when order does matter is calculated as follows:
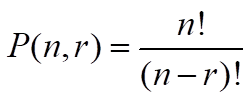
Combinations: The number of different arrangements of n things taken r at a time when order doesn’t matter:
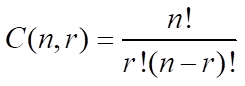
1. Probability they play each other in the first round
Since each player is equally likely to play another given player in the first round, the answer is the following:
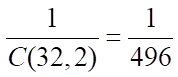
2. Probability they play each other at all
Firstly, it is important to note that there will be 31 games played which you can check for yourself below:
First round=16 games
Second round=8 games
Third round=4 games
Fourth round=2 games
Fifth round=1 game
16+8+4+2+1=31
Considering it is equally likely for the players to play the other player in any one of the games played during the whole tournament, the answer to part b is simply the answer to part a multiplied by the total number of games:
31*1/496=31/496
Final note
Although I recommend covering all bases on these methods and getting more practice on areas you feel weaker on, do not get overwhelmed or spend too much time stressing about brainteasers. Remember to balance other critical application components with brainteaser familiarity and mastery – this should prevent you from falling victim to the 80/20 rule where 80% of the results come from 20% of your efforts. Other critical application components to double down on include:
- Finalising or boosting your CV through completing online courses
- Networking to build relationships with people in the industry and gain invaluable insights the web struggles to rival
- Practising and documenting situational judgement or other psychometric tests
- Reinforcing and building your competency question responses
- Nailing your technicals
- Immersing yourself into building commercial awareness – potentially one of the most rewarding components of application season
- Focusing on your circle of influence in the face of rejection e.g. looking for more opportunities to apply to
As a side note, some of the brainteaser examples listed here are rarer for investment banking interviews as they generally appear in more quantitative roles, but the market sizing, calculations with multiple steps and mental maths questions are an absolute must that came up in many of the interviews I faced.